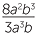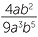Continuous

Continuous = is can be measured and take any value.


Cases:

• The tallness of a stallion (could be any esteem inside the scope of steed statures).

• Time to finish an errand (which could be measured to parts of seconds).

• The open air temperature at twelve (any esteem inside conceivable temperatures ranges.)

• The speed of an auto on Route 3 (accepting legitimate speed limits).

Example :

• person height 
• time in work
• a animal weight 

Graph: You can draw a ceaseless capacity without lifting your pencil from your paper.

Video 

Discrete

Discrete data is can be counted,can take certain values.


Example 1: number of people in city

Example 2: the results of rolling 2 dice:



can only have the values 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12

video Discrete and Continous

inequality

An inequality says that two values are not equal.

a ≠ b says that a is not equal to b

There are have special symbols that show below

Example 

Examples 1

Examples 2

Solve 2x - 5 < 12

Solution:

2x - 5 < 12

(2x - 5) + 5 < 12 + 5

2x < 17

(1/2)2x < (1/2)17

x < 17/2

Examples 3

Solve 13 - 3x  10

Solution:

13 - 3x  10

-3x  10 - 13

-3x  -3

(-1/3)(-3x)  (-1/3)(-3) (Recall - rule 5)

x  1

Exercise 1


 Solve the inequality z + 5 ≥ 3 and represent its solutions using a number line. 

Answer

z ≥ -2

Logarithm

A logarithm is the ability to which a number must be brought up so as to get some other number

Example 1

Log 100 = 2

Because

Example 2 

    How many 2 do we mutiply to get 16??

Answer: 2 × 2 × 2 x 2 = 16, so we needed to multiply 4 of the 2s to get 16

So the logarithm is 4

We write "the number of 2s we need to multiply to get 16s 4 as:

log₂(16)=4

Exercise :-

Number Pattern

list of numbers that follow a certain sequence.


Example: 1, 4, 7, 10, 13, ... starts at 1 and jumps 3 every time.

Another Example: 2, 4, 8, 16, 32, 64 ... doubles each time

Example

 Example: 27, 24, 21, 18, __

Note : (just -3 for the answer)

Example: 3, 4, 6, 9, 13, 18, __

Note : ( it must Add running number )

Combination

What number of various ways would you be able to choose 2 letters from the arrangement of letters: X, Y, and Z? (Indicate: In this issue, request is NOT critical; i.e., XY is viewed as an indistinguishable choice from YX.)

Arrangement: One approach to take care of this issue is to rundown the greater part of the conceivable determinations of 2 letters from the arrangement of X, Y, and Z. They are: XY, XZ, and YZ. Along these lines, there are 3 conceivable mixes.

Example 1

The group of different ways that a certain number of object as a group can be selected from a large object.

·         Order does not matter unordered list group

·         Choice, selection & election 

Permutation

Number of different ways that a certain number of object can be arrange in order from large number.

·         Order matters, an order matters

·         Key : arrangement

Indices

Introduction


Records are a helpful method for all the more just communicating extensive numbers. They additionally give us numerous helpful properties for controlling them utilizing what are known as the Law of Indices.


Law of Indices

• Six rules of the Law of Indices

Rule 1:



any power of zero (0) is equal to 1


examples:







Rule 2:


An Example:













Rule 3:




if the base is time, the power must be add.


An Example:









Rule 4:


if the base is divide, the power must be subtract.

An Example:










Rule 5:



To raise an expression to the nth index, copy the base and multiply the indices.


An Example:





Rule 6:



An Example:








Example Exercise:-


 ÷  = 6ab5.



Video - Video Indeses

Linear Programming

Maximising and minimising in linear function.

Subjected system of linear constraints. The constraints maybe equalities or inequalities . linear function is called the objective function of the f(x,y)= aX+ bY = c

The profit or cost function to the maximise or minimise the objective function. The process of finding the optimal level with the system of linear inequalities is called Linear Programing .

Object function the objective of linear problem to be maximise or minimise.

Example:  

                                Maximise : c = x + y

                               

      

 (Craig, 2015)




video 

Venn diagram

A Venn diagram is an illustration of the relationships between and among sets, groups of objects Usually, Venn diagrams are used to depict set intersections. The of diagram is used in scientific and engineering presentations, in theoretical mathematics, in computer applications, and in statistics.

a drawing is an example of a Venn diagram that are show the relationship among three overlapping sets X, Y, and Z. intersection relation is defined as the equal of the logic AND. An element is a member of the intersection of two sets. Venn diagrams are generally drawn within a large rectangle that denotes the universe, the set of all elements under consideration.




In this example, points that belong to none of the sets X, Y, or Z are gray. Points belonging only to set X are cyan in color; points belonging only to set Y are magenta; points belonging only to set Z are yellow. Points belonging to X and Y but not to Z are blue; points belonging to Y and Z but not to X are red; points belonging to X and Z but not to Y are green. Points contained in all three sets are black.


This is a practical example of how Venn diagram can illustrate a situation. Let the space be the set of all computers in the world. Let X represent the set of all notebook computers in the world. Let Y represent the set of all computers in the world that are connected to the Internet. Let Z represent the set of all computers in the world that have anti-virus software installed. If you have a notebook computer and surf the Net, but you are not worried about viruses, your computer is probably represented by a point in the blue region. If you get concerned about computer viruses and install an anti-virus program, the point representing your computer will move into the black area.


Exercise

find the shaded 

textbook = 5
Excises = 3
test = 2

Teaching = 10


answer  = ??